59 树到二叉树的转换
树到二叉树的转换
-
讨论中...... A:通用树结构的实现太复杂了...... B:通用树结构中的每个结点都可以有任意多的孩子,都可能具有无限形态,所以很复杂。 C:工程中很少能用到这么复杂的树,有没有简化的方案呢? D:减少结点中的孩子的数量应该就可以简化了吧,但这样简化后,树还能通用么?
-
通用树结构的回顾
- 双亲孩子表示法
- 每个结点都有一个指向其双亲的指针
- 每个结点都有若干个指向其孩子的指针
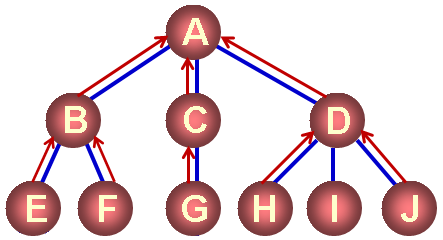
- 双亲孩子表示法
-
另一种树结构模型
- 孩子兄弟表示法
- 每个结点都有一个指向其第一个孩子的指针
- 每个结点都有一个指向其第一个右兄弟的指针
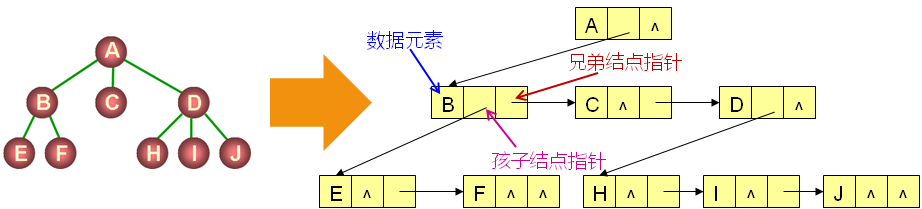
- 孩子兄弟表示法
-
孩子兄弟表示法的特点
- 能够表示任意的树形结构
- 每个结点包含一个数据成员和两个指针成员
- 孩子结点指针和兄弟结点指针构成了“树叉”
-
二叉树的定义 二叉树是有n(n≥0)个结点组成的有限集合,该集合或者为空。或者是由一个根结点加上两棵分别称为左子树和右子树的,互补相交的二叉树组成。
-
二叉树的五种形态
-
特殊的二叉树
- 满二叉树(Full Binary Tree) 如果二叉树中所有分支结点的度数都为2,且子叶结点都在同一层次上,则称这类二叉树为满二叉树。
- 完全二叉树(Complete Binary Tree) 如果一棵具有n个结点的高度为k的二叉树,他的每一个结点都与高度为k的满二叉树中编号为1——n的结点一一对应,则称这棵二叉树为完全二叉树。(从上到下,从左到右编号)
-
完全二叉树的特性
- 同样结点的二叉树,完全二叉树的高度最小
- 完全二叉树的叶结点仅出现在最下面两层
- 最底层的叶结点一定出现在左边
- 倒数第二层的叶结点一定出现在右边
- 完全二叉树中度为1的结点只有左孩子
小结
- 通用树结构采用了双亲结点表示法进行描述
- 孩子兄弟表示法有能力描述任意类型的树结构
- 孩子兄弟表示法能够将通用树转化为二叉树
- 二叉树是最多只有两个孩子的树
60 二叉树的深层特性
二叉树的深层特性
-
性质1
- 在二叉树的第i层最多有2i-1个节点。(i≥1)
- 第一层最多有21-1=1个结点
- 第二层最多有22-1=2个结点
- 第三层最多有23-1=4个结点
- ......
- 在二叉树的第i层最多有2i-1个节点。(i≥1)
-
性质2
- 高度为k的二叉树至多有2k-1个结点。(k≥0)
- 如果有一层,最多有1=21-1=1个结点
- 如果有两层,最多有1+2=22-1=3个结点
- 如果有三层,最多有1+2+4=23-1=7个结点
- ......
- 高度为k的二叉树至多有2k-1个结点。(k≥0)
-
性质3
- 对任何一棵二叉树,如果其叶结点有n0个,度为2的非叶结点有n2个,则有n0=n2+1。 证明:假设二叉树中度为1的结点有n1个且总结点为n个,则: n=n0+n1+n2 假设二叉树中连接父结点与子结点间的边为e条,则: e=n1+2n2=n-1 所以: n0=n2+1
-
性质4
- 具有n个结点的完全二叉树的高度为[log2n]+1。([x]表示不大于X的最大整数) 证明:假设这n个结点组成的完全二叉树高度为k,则: 2k-1-1<n≤2k-1 因为n为整数,所以: 2k-1≤n<2k 取对数: k-1≤log2n<k 因为k为整数,所以: k=[log2n]+1
-
性质5(这一条性质为完全二叉树所特有,普通二叉树不具备)
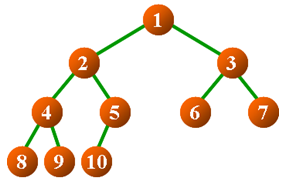
- 一棵有n个结点的完全二叉树(高度为[log2n]+1),按层次对结点进行编号(从上到下,从左到右),对任意结点i有:
- 如果i=1,则结点i是二叉树的根
- 如果i>1,则其双亲结点为[i/2]
- 如果2i≤n,则结点i的左孩子为2i;
- 如果2i>n,则结点i无左孩子
- 如果2i+1≤n,则结点i的右孩子为2i+1
- 如果2i+1>n,则结点i无右孩子
- 一棵有n个结点的完全二叉树(高度为[log2n]+1),按层次对结点进行编号(从上到下,从左到右),对任意结点i有: